|
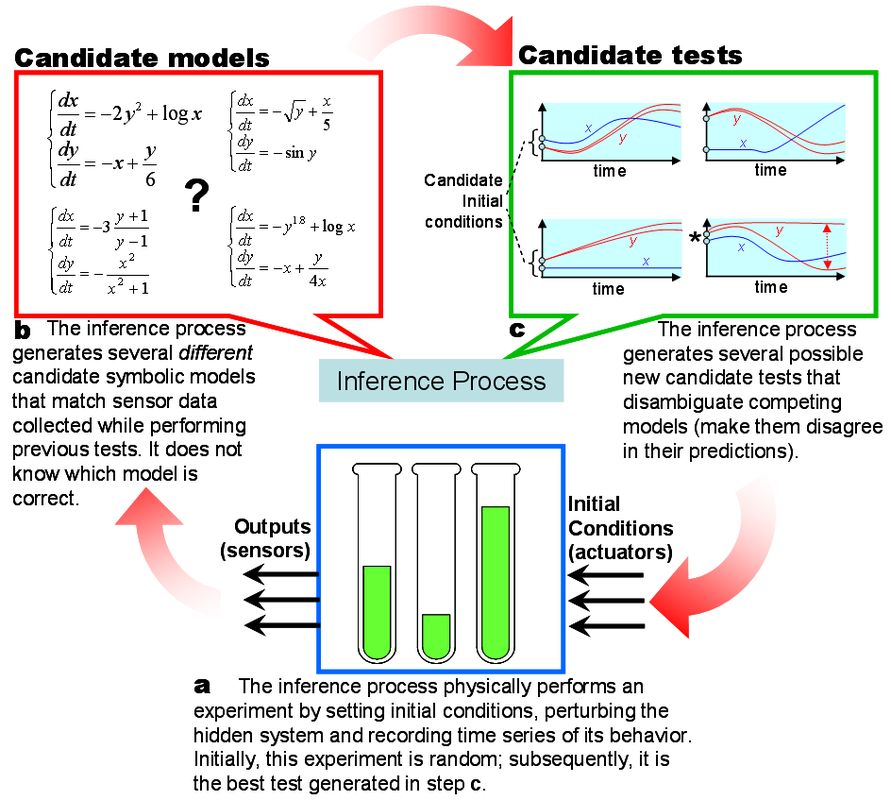
We introduce a method that can automatically generate sets of symbolic equations for a nonlinear coupled dynamical system directly from time series data. This method is applicable to any system that can be described using sets of ordinary nonlinear differential equations, and assumes that the time series of all variables are observable (possibly with some noise).
Previous automated symbolic modeling approaches of coupled physical systems produced linear models or required a nonlinear model to be provided manually. The advance presented here is made possible by allowing the method to model each (possibly coupled) variable separately, intelligently perturbing and destabilizing the system in order to extract its less observable characteristics, and automatically simplifying the equations during modeling. We demonstrate this method on four simulated and two real systems spanning mechanics, ecology, and systems biology. Unlike numerical models, symbolic models have explanatory value, suggesting that automated “reverse engineering” approaches for model-free symbolic nonlinear system identification may play an increasing role in our ability to understand progressively complex systems in the future. |
|
|
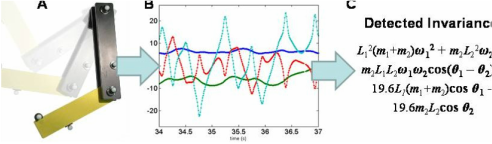
In 2009, we expanded this technique to discover also invariants. Mathematical symmetries and invariants are known to underlie nearly all physical laws in nature , suggesting that the search for many natural laws is inseparably a search for conserved quantities and invariant equations . Automated techniques for generating, collecting and storing data from scientific measurements have become increasingly precise and powerful, but automated processes for distilling this data into knowledge in the form of analytical natural laws have not kept pace. This trend is incommensurate with the rapidly increasing influx of scientific measurements coupled with the growing complexity of systems being studied. There is thus a pressing practical need for new forms of scientific data mining.
The most prohibiting obstacle to overcome in order to search for conservation laws computationally is finding meaningful and nontrivial invariants. Here we introduce a new principle for identifying useful analytical relationships. We then demonstrate how a search algorithm based on this principle identifies meaningful analytical relationships in data captured from a variety of physical systems. |
|
As a demonstration of our technique we developed Eureqa - a tool for searching analytical modeling of your own data. The tutorial on the right shows the basic operation of the original Eureqa software that was released in 2009. Since then, the technology has been spun out and developed commercially. It is now used by more than 40,000 users including many Fortune-500 companies.
Eureqa is available free for academic use. To learn more, visit Nutonian.com. |
|
Project participants |
|
Related Publications |
|